第2章 土の基本的性質および物理的性質
|
2.3 土の基本的性質
|
2.3.1 土粒子の密度と比重
一塊の土を、土粒子部分と間隙部分とに分けて模式的に図−2.0に示し
た。

図−2.0 土の組成模式図
土粒子の密度(γs)は、土の固相部分だけについての単位体積当りの重
量で、次のように表わされる。
γs=Ws/Vs(g/cm^3) ・・・・・・・・・・・・・・・・(2.1)
またある示された温度(T°C)において土粒子が空気中で示す重量(Ws)と、
ある示された温度(T°C)において土粒子と同体積の蒸留水が空気中で示す
重量(W')との比を土粒子の比重といい、ゲ−ルサック形比重ビンを用いて
測定するとき、土粒子比重Gs(T°C/T°C)は(2.2)式から求められる。

ここに Wa:温度T°Cの水を満たした比重ビンの重量(g)
Wb:温度T°Cの水と土とを満たした比重ビンの重量(g)
T°C:Wbをはかったときの比重ビンの内容物の温度
通常、物質の比重は4°Cの水に対する比重で表わされるが、土粒子の比
重は、特に指定のないとき、温度15°Cの水に対する比重Gs(T°C/15°C)
で表わしている。一般に土粒子の比重は、構成されている鉱物の種類や含有
程度によって異なるが、普通2.50~2.70程度の値である。また、得られる値
は、個々の土粒子あるいは代表鉱物の比重ということでなく、測定の対象と
なった土の土粒子全体の平均値ということである。土粒子の水中での沈降速
度などを算出する場合の計算のための数値として用いられる。
|
 |
|
 |
2.3.2 土の間隙率と間隙比
土を構成する各相の体積を、それぞれVs(固相)、Va(気相)およびVw
(液相)とすると、間隙部分の体積はVv=Va+Vw であり、土の前体積は
V=Vv+Vsで表わされる。
与えられた土の間隙の状態を量的に表わすのに、土の全体積に対する間隙
体積の比すなわち間隙率(%)、および固相の体積に対する間隙体積の比す
なわち間隙比を用いる。

(2.3)および(2.4)式において、土の全体積V実測することが容易であるが、
Vs の実測は困難である。したがって実測できる量、すなわち土粒子の重量
Ws と比重Gs とを知って、Vs=Ws/Gs・γw の関係からVs を計算から
求める。(2.3)式および(2.4)式はそれぞれ次のように書き換えられる。
n=(1−Ws/Gs・γw・V)×100、e=(Gs・γw・V/Ws)−1・・(2.5)
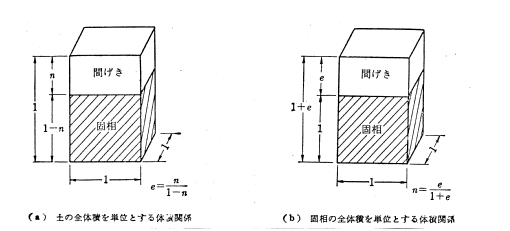
図−2.5 土の体積関係
図−2.5は、単位体積の土を考え、その全高さを(単位長さとして)1
とした場合と、土粒子(固相)部分の高さを1とした場合を示したものであ
る。図から、間隙の体積はVv=n・V、また土粒子体積はVs=(1−n)V
で表わされることがわかる。したがってeとnとの相互の関係は、次式のよ
うになる。
e=Vv/Vs=n/(1−n) 、n=e/(1+e)×100 ・・・・・・・(2.6)
nは百分率で、eは実数で表わすのが習慣となっている。たとえば間隙体
積と土粒子体積とが同じ(Vv=Vs)土では、e=0.5、n=50% というこ
とになる。間隙量として通常用いられるのは間隙比である。
間隙比は土の単位体積重量の計算、限界動水こう配の算定、土の透水性を
考える問題、圧密沈下の解析、および土の相対密度を求める場合などに用い
られる。
|
 |
|
 |
2.3.3 土の含水量
土の間隙中に含まれる水の量を含水量という。その量の表わし方として、
土の乾燥重量Ws に対する含水重量Ww の比(含水比)で表わす場合と、土
の湿潤重量Wに対する含水重量の比(含水率)で表わす場合とがある。
通常含水量は含水比で表わす。
W= Ww / Ws × 100 (%) (2.7)
自然状態における土の含水量を自然含水比と呼び、その含水量は、原位置
における土の強度やコンシステンシ−と深い関係をもっている。
土の含水量は、土の締固めの管理、土のコンシステンシ−限界を求める場
合、および土工・基礎工の安定を考える場合に用いられる。
含水量の測定法は、JSF T 121 に規定されている方法を標準としているが、
土工の施工管理や、すばやくそのときの含水量を知る必要のある場合に、迅
速測定法として、アルコ−ル燃焼法・赤外線乾燥法・高周波乾燥法など、い
ろいろな方法が用いられている。
|
 |
|
 |
2.3.4 飽 和 度
土の間隙中、水の占めている割合を表わすのに飽和度Sr あるいは相対含
水比という語が用いられている。飽和度とは、土の全間隙体積Vv に対する
間隙中の水の体積Vw の比(または百分率)として次式のように表わされる。

ここに Ww:間隙中の水の重量
Wv:全間隙を満たしたときの水の重量
w:含水比
wsat:全間隙を水で満たしたときの含水比
また、間隙率で表わすと次式のようになる。
Sr=nw/n ・・・・・・・・・・・・・・・・(2.9)
飽和度によって土の相構成および間隙の状態は次のように分けられる。
(1)Sr<1 : 不飽和の状態を示す。固相−液相−気相の3相構成
(2)Sr=1 : 間隙が完全に水で満たされた飽和の状態を示す。
固相−液相の2相構成
(3)Sr=0 : 完全乾燥の状態を示す。固相−気相の2相構成
表−2.1は、飽和度による土の状態を区分したものである。

|
 |
|
 |
2.3.5 土の単位体積重量
土の単位体積当りの重量を、土の単位体積重量あるいは密度という。重量
として、土粒子重量と間隙中の水の重量とを合わせて考える場合(W=Ww
+Ws)を湿潤単位体積重量γt(あるいは湿潤密度)といい、土粒子重量Ws
だけを考える場合を、乾燥単位体積重量γd(あるいは乾燥密度)といって次
のように表わす。

土の単位体積重量は、土の状態が同じであっても飽和条件および水に浸さ
れているかどうかによって変わってくる。今、土粒子の比重Gs と土の間隙
比eが既知である場合の各種条件下での土の単位体積重量を考えてみよう、
図−2.6からわかるように、Sr=0(完全乾燥状態)の場合には、土の全

体積V=1+eに対して、固相の重量がWs=Gs・Vs・γw で、この場合Vs
=1であるから、土の乾燥単位体積重量γdは、

で表わされる。間隙が水で満たされた場合、すなわち飽和の状態では、土
の全重量はe・γw+Gs・γwであり、土の全体積は上と同じくV=1+eで
あるから、飽和条件下での土の単位体積重量γsatは

となる。
(2.11a)式と(2.11b)式を比べてみるとわかるように、間隙体積が一定であ
る土では、間隙中の水の変化によって土の単位体積重量は変化する。乾燥単
位体積重量は、その土のその状態における最小の密度であり飽和された場合
はその密度が最大となる。
地下水下にある土のように水で浸されている場合は、同体積の水の重量に
相当する浮力を受けているので、水浸されている土の単位体積重量γsubは、
飽和条件における単位体積重量γsatから、水の単位体積重量γwを差し引い
たものとなる。
すなわち、

土のeあるいはn、Gsおよびγwが既知である場合に、飽和の状態によっ
て変わる単位体積重量を求める式を一括して表−2.2に示してある。

|
 |
|
 |
2.3.6 土の物理定数および相状態定数相互の関係
土の基本的性質を表わす物理的定数や土の状態定数については、すでに述
べているが、ここでは物理定数および各相の相互の関係をとりまとめて述べ
る。

図−2.7は、土の各相の重量および体積の絶対量と相対量とを、それぞれ
総合して表わしたものである。 いま、既知の量あるいは実測しうる量とし
て、γw、Gs、Ws、WおよびVがわかると、各相の絶対量と、それらの相互
の割合は次のような計算から求まる。
a.各相の絶対量
(1)水の重量 :Ww=W−Ws
(2)土粒子の体積 :Vs=Ws/Gs・γw
(3)間隙の体積 :Vv=V−Vs=V−Ws/Gs・γw
(4)水の占める間隙体積 :Vw=Ww/γw
(5)空気間隙体積 :Va=Vv−Vw
b.相互の重量および体積

|
 |
|
|
[ ↑目次へ戻る ]
|
 |
